 表計算ソフトからは、コピー&ペーストでグラフ化できる
表計算ソフトからは、コピー&ペーストでグラフ化できる
グラフ作成に表計算ソフトを使用する場合、値の入力されている領域を選択してコピーし、 リニアングラフ3Dの画面上で右クリックして、メニューから「Paste Data」を選ぶことで、 ファイルを作らずにそのままグラフにプロットできます。
ここでは、リニアングラフ3D で読み込み可能なファイルの書式(記述方法)について説明します。 ここでの書式に基づいて座標値ファイルを作成してください。
 表計算ソフトからは、コピー&ペーストでグラフ化できる
表計算ソフトからは、コピー&ペーストでグラフ化できる
グラフ作成に表計算ソフトを使用する場合、値の入力されている領域を選択してコピーし、 リニアングラフ3Dの画面上で右クリックして、メニューから「Paste Data」を選ぶことで、 ファイルを作らずにそのままグラフにプロットできます。
- 目次 -
グラフ用の座標値ファイルには、座標値を並べた数列を記述します。
このように数列をファイルに記述するには、CSV とTSV という2 つのファイル形式があります。
グラフ作成において、CSV は表計算ソフトで作成するデータなどでよく使用され、 TSV はプログラミング言語などで作成するデータなどでよく使用されます。 リニアングラフ3D では、CSV とTSV の両方に対応しています。
CSV/TSV といった区切り文字の書式の他にも、グラフ用のデータには「数列をどう並べるか」といった点について、複数の書式が存在します。
リニアングラフ3D では、一般的に広く使用されている「マトリックス書式」及び「3 カラム書式」に対応しています。 ここではまず、前者について解説します。
「マトリックス書式」とは、縦方向(行)をX 値、横方向(列)をY 値と見なし、 行列のようにZ 値を記載していく書式です。マトリックス書式は、表計算ソフトなどで簡単に作成可能というメリットがあります。 反面、X やY が格子状に並んだ座標しか表現できないというデメリットもあります。
以下に、表計算ソフトでマトリックス書式のファイルを作成する手順を例示します。
まず表計算ソフトウェアを起動し、最も左上のセルを空白にしたまま、最も左側の列にX値を記述し、最も上側の行にY値を記述します。 そして、このX列とY行を辺とする長方形領域に、各X・Y に対応するZ 値を記述します。
図:表計算ソフトウェアの記述例
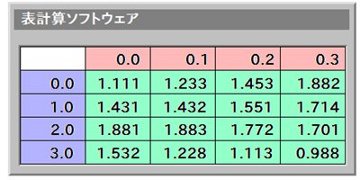
上図において、青い列がX 値、赤い行がY 値、緑の領域がZ 値を意味します。 上図のように記述し、ファイルをCSV(カンマ区切り)形式で保存してください(タブ区切りのTSV形式で保存しても問題はありませんが、 この書式ではCSV を推奨します)。作成されたCSV ファイルは、リニアングラフ3D で読み込む事ができ、 面プロットを含む全てのプロットオプションが使用可能です。
なお、必要が無ければX 列とY 行の記述は省略する事が可能です。 その場合はZ 値の領域(上図において緑の領域)を、最も左上のセルから詰めて記述してください。 その場合、X 値とY 値にはそれぞれ列番号と行番号が割り振られます。
リニアングラフ3D では、最も左上のセルに「 LEVEL_INDEX 」と記載すると、 複数系列が定義されたマトリックス書式として読み込まれます。このセルの左から順に、1行目に系列番号を記載します。
2 行目以降は、通常のマトリックス書式と同様です。ただし1行目に記載した系列番号により、 座標値の所属する系列が振り分けられます。系列はいくつでも使用可能です。
※なお、面プロットを使用するには、各系列においてX 及びY が昇順もしくは降順に並んでいる必要があります。
図: 複数系列におけるマトリックス書式の記述例(表計算ソフト使用)
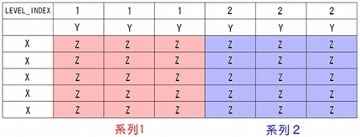
上図において、一行目が系列番号と見なされます。系列が異なる座標値は別のグラフとして表現されます。系列の異なるデータは、グラフ化した際に別の色で彩色されます(※With RainbowオプションOFF 時)。
表計算ソフトにおいてマトリックス書式がよく使用されるのに対して、プログラミング言語を用いた分野では、
3 カラム書式がよく使用されます。3 カラム書式はファイル各行に左からX、Y、Z と記載し、1 行につき1 個の座標点を表現する書式です。
この書式は、プログラミングにより非常に効率的に作成できる事、 及びX やY が格子状に並ばない自由な座標値を表現できる事がメリットとして挙げられます。 このメリットから、表計算ソフトでのデータ作成においても使用される事があります。
3 カラム書式の例:3 カラム形式では、空白行を挟む事により、複数のデータを一枚のファイルに記載する事が容易にできます。 リニアングラフ3D では、2 行連続した空白行をはさむと、そこが系列の区切りと見なされ、 そこ以降は別の系列に属するデータと見なされます。系列の異なるデータは、 グラフ化した際に別の色で彩色されます(※With Rainbow オプションOFF 時)。
3 カラム書式で面を表現するには、まずY 値を固定し、X 方向に沿って端から端まで座標値を書き出してください。 そこで空白改行を1 行はさみ、Y 値を1 つ進め、またX 方向に沿って端から端まで座標値を書き出してください。 これを繰り返して面全体の座標値を書き出してください。
例として、次ページにある図のような、3×3 メッシュ上における面Z(X,Y)を表現する座標値データを以下に示します。
図:3×3の格子点(各格子点にZ値が対応)
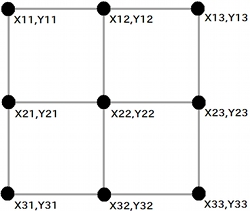
このような座標値ファイルを出力する、C++言語及びFORTRAN77 言語での簡単なプログラムを以下に例示します。
以下は、Z = sin( X )+cos( Y ) の曲面グラフを作成する、C言語でのプログラムの例です。
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main(void) {
double x, y, z;
int xi, yi;
int xN = 10; // X 方向の座標点数
int yN = 10; // Y 方向の座標点数
// X・Y 方向の計算範囲
double xMin = -5.0;
double yMin = -5.0;
double xMax = 5.0;
double yMax = 5.0;
// 出力ファイルを開く
FILE *fp = fopen("a.tsv", "w");
if (fp == NULL) {
fprintf(stderr, "failed to open the file");
return EXIT_FAILURE;
}
for( yi=0; yi<yN; yi++ ){
for( xi=0; xi<xN; xi++ ){
x = ( xMax - xMin ) * xi / (xN-1);
y = ( yMax - yMin ) * yi / (yN-1);
z = sin(x) + cos(y);
// 値をタブ区切りで書き出して改行
fprintf(fp, "%lf\t%lf\t%lf\n", x, y, z);
}
fprintf(fp, "\n"); // 空白改行
}
return EXIT_SUCCESS;
}
以下は、Z = sin( X )+cos( Y ) の曲面グラフを作成する、C++でのプログラムの例です。
#include <fstream>
#include <cstdlib>
#include <cmath>
int main(){
double x, y, z;
int xN = 100; // X 方向の座標点数
int yN = 100; // Y 方向の座標点数
// X・Y 方向の計算範囲
double xMin = -5.0;
double yMin = -5.0;
double xMax = 5.0;
double yMax = 5.0;
// 出力ファイルを開く
std::ofstream ofs( "a.tsv" );
for( int yi=0; yi<yN; yi++ ){
for( int xi=0; xi<xN; xi++ ){
x = ( xMax - xMin ) * xi / (xN-1);
y = ( yMax - yMin ) * yi / (yN-1);
z = sin(x) + cos(y);
// 値をタブ区切りで書き出して改行
ofs<<x<<"\t"<<y<<"\t"<<z<<std::endl;
}
ofs<<std::endl; // 空白改行
}
ofs.close();
return EXIT_SUCCESS;
}
以下は、Z = sin( X )+cos( Y ) の曲面グラフを作成する、VCSSLでのプログラムの例です。
import Math ;
double x ;
double y ;
double z ;
int xN = 100; // X方向の座標点数
int yN = 100; // Y方向の座標点数
// X・Y方向の計算範囲
double xMin = -5.0;
double yMin = -5.0;
double xMax = 5.0;
double yMax = 5.0;
int file = open ( "a.tsv", "wtsv" ); // 出力するファイル(wtsvはTSV書き込みモード)
for( int yi=0; yi<yN; yi++ ){
for( int xi=0; xi<xN; xi++ ){
x = ( xMax - xMin ) * i / (xN-1) ;
y = ( yMax - yMin ) * j / (yN-1) ;
z = sin(x) + cos(y) ;
// X,Y,Z値をタブ区切りで書き出して改行
writeln( file, x, y, z ) ;
}
writeln( file, "" ) ; // 空白改行
}
close( file )
以下は、Z = sin( X )+cos( Y ) の曲面グラフを作成する、FORTRAN 77 でプログラムの例です。
IMPLICIT NONE
REAL*8 X,Y,Z,X_MAX,Y_MAX,X_MIN,Y_MIN
INTEGER X_I,Y_I,X_N,Y_N
X_N = 100 ! X 方向の座標点数
Y_N = 100 ! Y 方向の座標点数
X_MAX = 5.0D0 ! X 方向の計算範囲
X_MIN = -5.0D0 ! X 方向の計算範囲
Y_MAX = 5.0D0 ! Y 方向の計算範囲
Y_MIN = -5.0D0 ! Y 方向の計算範囲
OPEN(UNIT=14,FILE='a.tsv',STATUS='UNKNOWN')
DO Y_I = 0, Y_N
DO X_I = 0, X_N
X = (X_MAX-X_MIN)*DBLE(X_I)/DBLE(X_N-1)
Y = (Y_MAX-Y_MIN)*DBLE(Y_I)/DBLE(Y_N-1)
Z = SIN(X) + COS(Y)
! X,Y,Zをタブ区切りで書き出して改行
WRITE(14,*) X, Y, Z
ENDDO
WRITE(14,*) ! 空白改行
ENDDO
CLOSE( 14 )
STOP
END