ここでは、表示する桁数の設定や、各演算モード時の精度について説明します。 リニアンプロセッサーは、VF モードを使用する事で、大きな桁の演算も扱う事ができます。
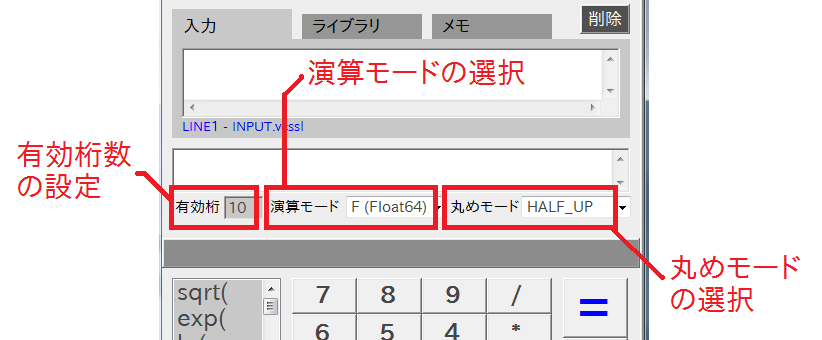
「出力」欄の下で、桁数や演算モード、および丸めモードを選択できます(下図)。

有効桁数とは、簡単に言うならば 「 先頭から数えて何個有効な数字が続くか 」 という桁数です。 厳密な解説はここでは割愛しますが、例えば 1.2345 も 123.45 も有効桁数は 5 桁です。
一般に、割り切れないような計算は何桁でも数字が続きますが、計算結果が表示される際には、 「出力」欄の左下にある「 有効桁 」項目で設定した有効桁数に揃えられます。
なお、綺麗に割り切れる計算などで、計算結果の桁数が、設定された桁数よりも少なくなる場合も あります。そのような場合、標準設定では、少ないままの桁数で表示されます。 もし、末尾に 0 の列を追加して、強制的に設定された桁数まで揃えたい場合 (つまり有効桁数が何桁であるかを強調したい場合)は、 「 設定 」 メニューの 「 ゼロ揃え 」 項目を有効にしてください。
上で述べたように、「有効桁」項目の設定値は有効桁数であって、 いわゆる「 小数点以下が何桁か 」 というような桁数とは全く無関係です。
計算結果を、小数点以下の決まった桁数で切り揃えたい場合(固定小数点表示)は、 「 設定 」 メニューの 「 固定小数点表示 」 項目を有効にしてください。 すると、「有効桁」項目があった場所(VF モード時はその下)、 下に 「少数桁」 項目が出現するので、ここで小数点以下の桁数を指定してください。
なお、固定小数点表示は、結果を小数点以下の決まった桁で “ 切り揃えて ” 丸めるだけです。 なので、例えばそもそも計算結果において小数点以下 2 桁までしか数字が無いのに、 少数桁項目で小数点以下 5 桁までに設定したとしても、 もともと数字が無いので小数点以下 2 桁までしか表示されません。
従って VF モード時などには、もともとの有効桁数も足りるように設定しておく必要があります。 ただし、有効桁数を大きく設定しても、「(1 以下の部分という意味での)小数点以下」が何桁になるかは、 計算する内容によって異なるのでご注意下さい(コンソール上の表示値で確認できます)。
計算結果を、設定された有効桁数に揃える際、端数がどのように丸められるかは、 「出力」欄の右下にある「 丸めモード 」項目で選択します。 例えば「 UP 」を指定すれば切り上げ、「 DOWN 」を指定すれば切り捨てを行います。
それ以外の 「 HALF_〜 」 のどれかを指定した場合、 値によって切り上げか切り捨てのどちらかが行われ、最も近い数値に丸められます。 例えば設定桁以降の端数が 500…1 と続くなら切り上げ、499…9 と続くなら切り捨てが行われます。 ただし、設定桁以降の端数がちょうど 500…0と続く場合、 切り上げと切り捨てのどちらが近いというわけでもありません。 このような場合をどのように扱うかは、「 HALF_〜 」のどれを指定するかで異なります。
「 HALF_UP 」を指定すれば、設定桁以降の端数が 500…0 と続く場合は切り上げられます。 そして設定桁以降が 499…9 と続く場合は切り捨てられます。 つまりこの場合、設定桁の次の桁を(それ以降の桁は無視して)四捨五入したのと同様の結果が得られます。
「 HALF_DOWN 」を指定すれば、設定桁以降の端数が 500…0 と続く場合は切り捨てられます。 そして 500…1 と続く場合は切り上げられます。
「 HALF_EVEN 」を指定した場合は少し特別です。 この場合では、設定桁以降の端数が 500…0 と続くとき、切り上げるか切り捨てるかは、 その前の桁が偶数か奇数かによって反転します(偶数方向へ丸めます)。
なお、「 NONE 」を指定した場合は丸めを行わず、内部処理における演算結果をそのまま返します。 演算結果を自分で丸めたい場合に使用して下さい。 なお「 NONE 」の場合は、指定された桁数にはならず、 ゼロ揃え等のオプションも効きません。つまり、結果の値に何も行われません。
少しコンピュータの仕組みに関わる内容になりますが、リニアンプロセッサーにおける数値の演算は、 標準(F モード)では 「 2 進数 64bit 浮動小数点数 」 という形式で扱われます。 これはコンピュータにおいて非常に高速に計算できる形式で、 10 進数換算で約 16 桁前後の値を扱えます(ただし、2 進数特有の誤差を考慮する必要があります)。
場合によっては、16桁を超える大きな桁数の小数を扱いたい場合や、 2進数誤差を嫌って10進数で演算してほしい場合もあります。 また、小数ではなく整数として演算してほしい場合もあるでしょう。 こういった様々な用途に対応するため、リニアンプロセッサーには、以下の 3 つの 「 演算モード 」 が存在します。
| 演算モード | 説明 |
|---|---|
| F ( float64 ) | すべての入力値を約 16 桁の小数(2 進 64bit 浮動小数点数)として扱います。 |
| VF ( varfloat ) | すべての入力値を任意桁の小数(10 進多倍長浮動小数点数)として扱います。 |
| DIRECT |
整数や小数など、異なる種類(型)の値を混在して扱います。 型は C 言語系の数値リテラル表記で判断されます。 例えば整数なら、「123」は 10 進数、「0b101」は 2 進数、「0o123」は 8 進数(※)、 「0x123abc」は 16 進数とみなされます。 「1.23」は 64bit 浮動小数点数、「1.23vf」は多倍長浮動小数点数となります。 ※ 8 進数リテラルについては、バージョン 4.2 までは 「 0(ゼロ)を頭に付ける 」 という標準的なルールを採用していましたが、慣れない場合の混乱を防ぐため、 バージョン 4.3 以降では「 0o(ゼロ・オー) 」を頭に付けるという記法に移行しました(VCSSL も同様です)。 従来の記法も使用できますが、警告メッセージが表示されます。 表示したくない場合は「設定」メニューから「互換性に関する警告を無視」を有効にしてください。 |
普通の電卓として特に重要なのは F モード(標準)と VF モードでしょう。 これらは両者とも小数の演算を行うモードですが、 精度(有効桁数の限界など)と処理速度が大きく異なります。 詳しい特徴は次表をご参照ください。
下の表は、一般的な用途向けである、F モードと VF モードの特徴について詳しくまとめたものです。
| F モード(標準) | VF モード | |
|---|---|---|
| 概要 | 内部処理に 64bit の 2 進数が使用されます。 最大 16 桁程度まで扱えます。 非常に高速で、数学関数も軽快で正確です。 反面、末尾の数桁に、2進数演算に特有の誤差などが生じます。 | 内部処理に任意桁数の 10 進数が使用されます。 何桁でも扱えて、高精度です。 反面、大きな桁数では、処理速度が低下します。 特に数学関数は独自開発ライブラリのため、比較的重く、 精度検証もまだ完全ではありません。 |
| 演算精度(桁) | 限界で 16 桁程度です。信頼できるのは14桁程度で、 現実的には、安全マージンを取ると 10 桁程度です。 | 任意桁数なので、必要に応じていくらでも桁数を増やせます。 ただし桁数を増やすと、演算速度は低下します。 |
| 内部処理の型 | 64bit, 2進数( double ) | 多倍長, 10進数 |
| 内部処理における丸め(※) | 開発言語 に お け る 組 み 込 み 型( double ) の丸め処理がそのまま使用されています。 | Ver.4.2.48(VCSSL 3.3.12)以降から段階的に Half-even に移行中です。それ以前は単純な切り捨てです。 |
| 想定すべき誤差など | 10進/2進変換に特有の誤差などに注意が必要です。 末尾の数桁には常に誤差が含まれると考えるべきです。 | 10 進/2 進変換の誤差を気にする必要はありません。 ただしあくまで有限桁なので、丸め誤差などは存在します。 |
| 演算速度 | 100 M FLOPS程度( 数億回 / 秒 ) | 最大1 M FLOPS程度( 最大数百万回 / 秒 )、桁数が大きくなると遅くなります。 |
| 数学関数 | 高速で正確です。 ※ ただし、一般のプログラミングでの数学関数の使用時と同様、 必ずしも 64bit の限界までの精度が出るわけではなく、精度は関数によります。 | 歴史の浅い、独自開発のライブラリを使用しているため、 比較的低速であり 、精度検証も完全ではありません(使用前のテストが推奨されます)。 その代わり、sin 関数の値を千桁求める等、 普通の電卓では不可能なほどの長い桁数の値を求める事が可能です。 |
※ ここでの「内部処理における丸め」とは、先に述べた「丸めモード」の設定項目とは無関係であり、 「内部で演算を行う際の丸め」の事を意味します(内部処理では、設定桁数よりも余裕を持った桁数で演算が行われます)。 そうして演算を行った最終的な結果が、「丸めモード」で設定した方法で、設定桁数に丸められて表示されます(後述)。
さて、上の表では、精度や誤差など、細かい点が色々と記載されていますが、 10 桁程度の計算で、小数を普通に扱うような場合であれば、 このような点をあまり気にし過ぎる必要は無いでしょう。
なぜならリニアンプロセッサーは、内部処理では設定桁数よりも大きな桁数で演算を行い、 結果表示時に指定桁まで丸めてから、「出力」欄に出力するからです。 例えば、Fモードで有効桁が10桁に指定された状態で、以下の数式を計算してみましょう。
- 入力 -1.01 - 0.001
1.009
1.01-0.0010
[ 1.01-0.0010 = 1.0090000000000001 ]
1.0090000000000001
さて、コンソールに注目してください。
この場合、内部処理では17桁の結果が得られた事が分かります。 そして、その最終桁は、本来「 0 」であるべきなのに「 1 」になっている 事が見て取れます(これはコンピューターで2進数で小数点付きの数値を処理する事に起因する、有名な誤差の一種によるものです)。 こういった誤差は、内部処理における末尾桁の数桁まで影響する可能性があります。
しかしながら、結果は 10 桁に四捨五入(丸めモードに依存)されてから出力されたため、 末尾の誤差「…001」の影響は切り捨てられた事が分かります。
上のように、多くの場合は丸めによって補正されますが、 しかしながら、F モードにはこういった類の誤差が常に存在するという事は、 あらかじめ認識した上で使用して下さい。 そして、これが問題となる場合には、小数演算では VF モード、整数演算では DIRECT モードなどを使い分けて下さい。
F モード時には、内部処理でも最大で 16〜18 桁までしか扱えないため、 10 桁よりも大きい桁数で計算させる際は注意が必要です。 極端な例では、F モード時に 16 桁などで計算させると、桁数がギリギリで丸める余地が無くなってしまい、 誤差が結果に見える領域に現れる可能性があります。
どうしてもそのような大きな桁数を扱いたければ、VF モードを使う事が推奨されます。VF モードでは、 内部処理で無制限に桁を使えるため、ちゃんと安全マージンを取って計算した上で、丸めて表示する事ができます。 実際、先ほどの例では、VF モード時の場合、16 桁に設定しても内部ではより大きな桁数で計算され、 16 桁に丸められます(丸めモードに依存、標準の HALF_UP 時は四捨五入されます)。
また、VF モードでは数千桁の計算も扱う事ができます。例として、VF モードを使い、 桁数を 1000桁に指定して、以下の数式を計算してみてください。( 少し時間がかかります )
- 入力 -このように、1000 桁の正しい値を得る事ができました。
ただし、VF モード時における数学関数の処理には、 まだ歴史の浅い、独自開発のライブラリが使用されています。 そのため、あらゆる入力値と桁数について、精度が完全に確認されているわけではありません。
VF モードで数学関数を使う場合、厳密性を要求されるような場面では、 上のように結果が分かっている数式を用いて、予め動作検証を十分に行う事が推奨されます。