

Last month, as we introduced in the following article, we released an open-source expression calculator library "Exevalator", available in Java®/C#/C++/Rust.
» News 2022/04/16: Released "Exevalator": A Multilingual & Copyright-Free Expression Evaluator Library
Source code of Exevalator is copyright-free, so you can customize/divert it freely. Hence, in this article, for reference when you read/modify source code, we explain internal architecture of Exevalator.
By the way, our explanation in this article is based on of Exevalator's source code implemented in Java. Structure of implementations in other languages (C++, C#, Rust) are roughly the same, but may be little different.
First of all, to grasp the whole internal structure, see the following block diagram:
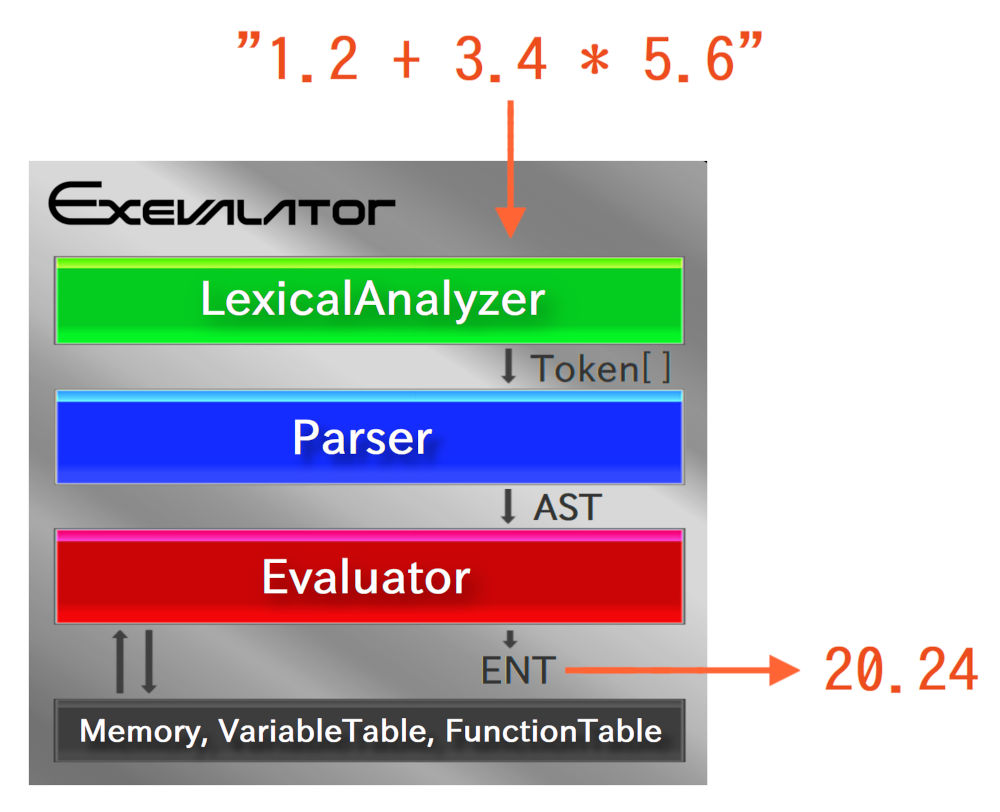
As the above, Exevalator consists of three major components:
In addition, we recommend to keep the following elements in the back of your mind:
The above three elements are not so important, compared with the first three components (Lexical Analyzer, Parser, Evaluator), so packed in one block in the block diagram. But in the latter part of this article, when we explain how variables/functions are accessed/called, it requires to recall the above elements.
That's all for whole structure. Let's zoom in on each component. Now, we assume that now the following expression is inputted to Exevalator:
How Exevalator calculates this expression internally? Let's zoom in on each component.
The above expression will be inputted to the first component: Lexical Analyzer. In source code, it is implemented as a "LexicalAnalyzer" class. The expression will be passed to its "analyze" method, as a String-type argument.
Then the LexicalAnalyzer splits the content of the expression into tokens, and returns them as an array of Token-type objects:
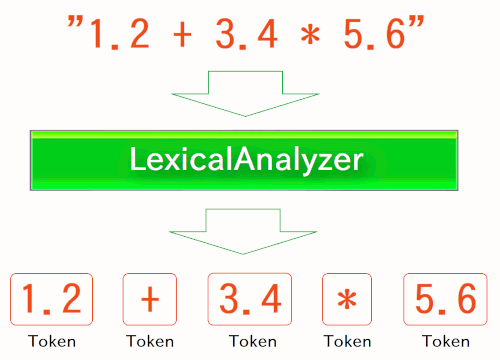
where "tokens" are symbols, numeric values, and other words (e.g.: names of variables/functions), composing the expression.
Next, tokens will be inputted to Parser. In source code, it is implemented as "Parser" class, and tokens will be passed to its "parse" method as an (array) argument. Then the Parser constructs AST (Abstract Syntax Tree) from tokens, and returns the root node of it, as an AstNode-type object:
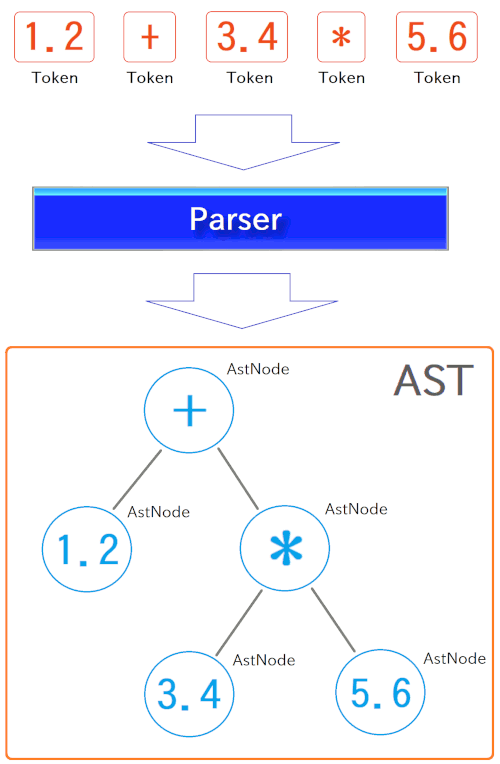
where AST is, roughly speaking, a tree-shape object representing syntactic relationships/roles of all tokens in a expression (or code, in general).
For example, if you "interpret" the meaning of "1.2 + 3.4 * 5.6" as "(1.2 + 3.4) * 5.6", you will get the different value from when you interpret it as "1.2 + (3.4 * 5.6)". On the most languages (containing Exevalator), it will be interpreted as the latter, because multiplications have precedence over additions.
Hence, it requires to analyze that: "This '*' means multiplication of 3.4 and 5.6, and this '+' means addition of 1.2 and the result of the multiplication, and ...". This is role of the Parser.
AST can represent the above result of syntactic analysis well, as an tree-shape object.
The next is the last major component: Evaluator.
The Evaluator is the component to evaluate the value of AST, but it has a little complex structure for improving performance. So Let's start this section from more general explanation of: how we can evaluate (calculate) the value of an AST.
If you don't worry about processing speed, you can calculate the value of an expression from its AST very easily, as follows:
Traverse all nodes in the AST, and calculate the value of each node, in the order from the bottom (leaf) to the top (root). Where the value of an operator's (+, *, etc.) node is the operated result value, of which operands are values of child nodes. The value of a number literal's (a constant value directly written in the expression) node is the literal value itself. The value of a variable's nodes is gotten by reading the value in the memory, at the address of the variable.
See the following figure. It is easy, isn't it?
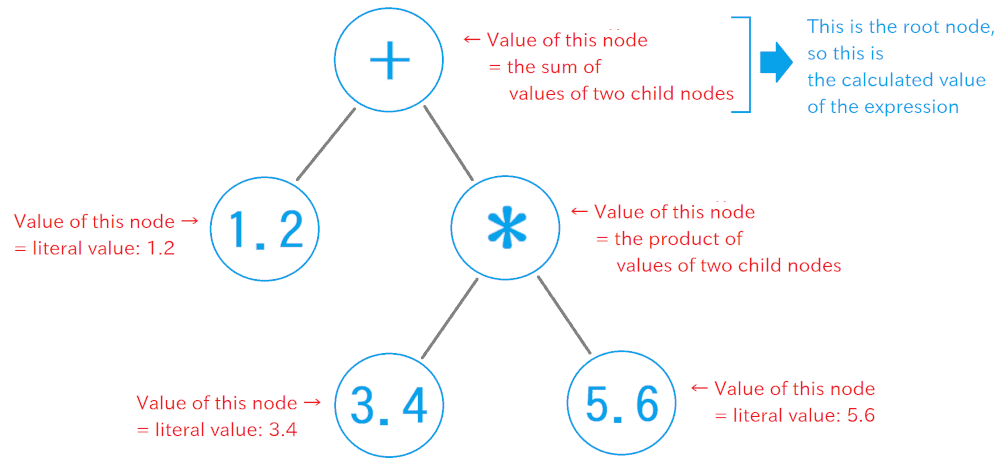
Most simple way to implement the above behaviour is: Traversing all nodes by using a loop or recursive calls, and take the suitable process depends on the type of each node, by using "if" or "switch" statements. This kinds of interpreters are called as "Tree Walker" in general.
Naive implementation of a tree walker requires the CPU to process many branch instructions, for each nodes. It will be a relatively heavy bottleneck if you want to make your interpreter faster. Hence, "interpreter enthusiasts" try to eliminate branch instructions from their interpreters as possible as, by using function pointers, dynamic dispatch, and so on (one of the ultimate way is JIT).
In the point of view to reduce overhead costs of branch instructions, the Evaluator calculates the value of an AST in little elaborate way.
Specifically, in Evaluator, many subclasses of "EvaluatorNode" class are defined. EvaluatorNode class has an abstract method: "evaluate". Behaviour of "evaluate" method of each EvaluatorNode's subclass is overridden, for performing processes suitable for the type of each AST node. Instances of EvaluatorNode's subclasses will be linked into the same tree-sahape as an AST. We call it as ENT (EvaluatorNode Tree) in this article (Note that, it is non-general name):
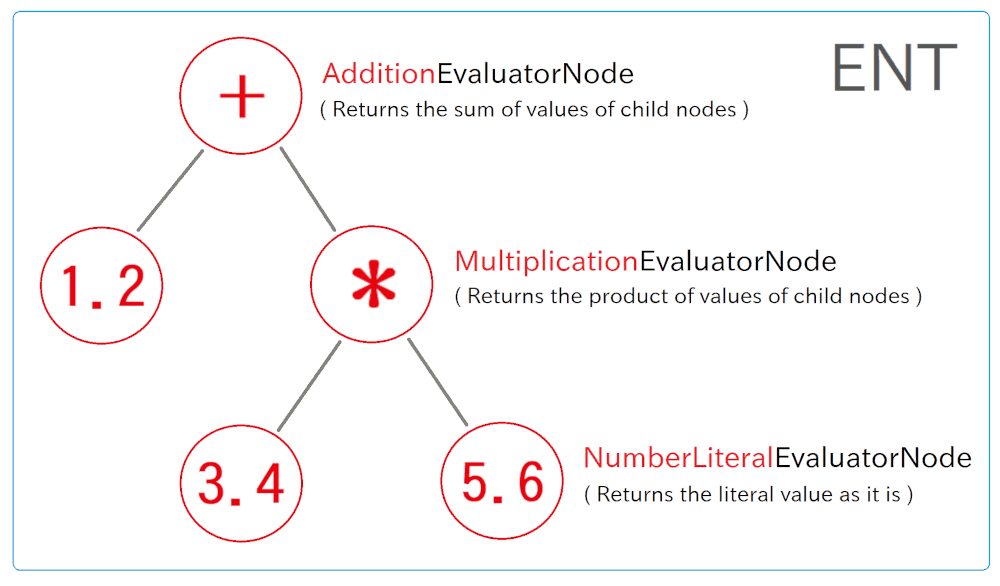
As the above figure, "evaluate" method of "AdditionEvaluatorNode" class returns the value of additions of two child nodes. "MultiplicationEvaluatorNode" returns the value of multiplications of two child nodes. "NumberLiteralEvaluatorNode" returns the constant literal value.
When you call "execute" method of the root node of the ENT, "AdditionEvaluatorNode" in the above case, the processing flow traverses in all nodes of the ENT recursively, and the value of each node propagates from the bottom to the top. So you will get the value of whole expression as the return value of the root node of ENT.
Does it make sense? Let's get back on topic: the processing flow in Exevalator. When an AST is inputted to the Evaluator, it construct an ENT corresponding the AST, and returns the root node of the ENT.
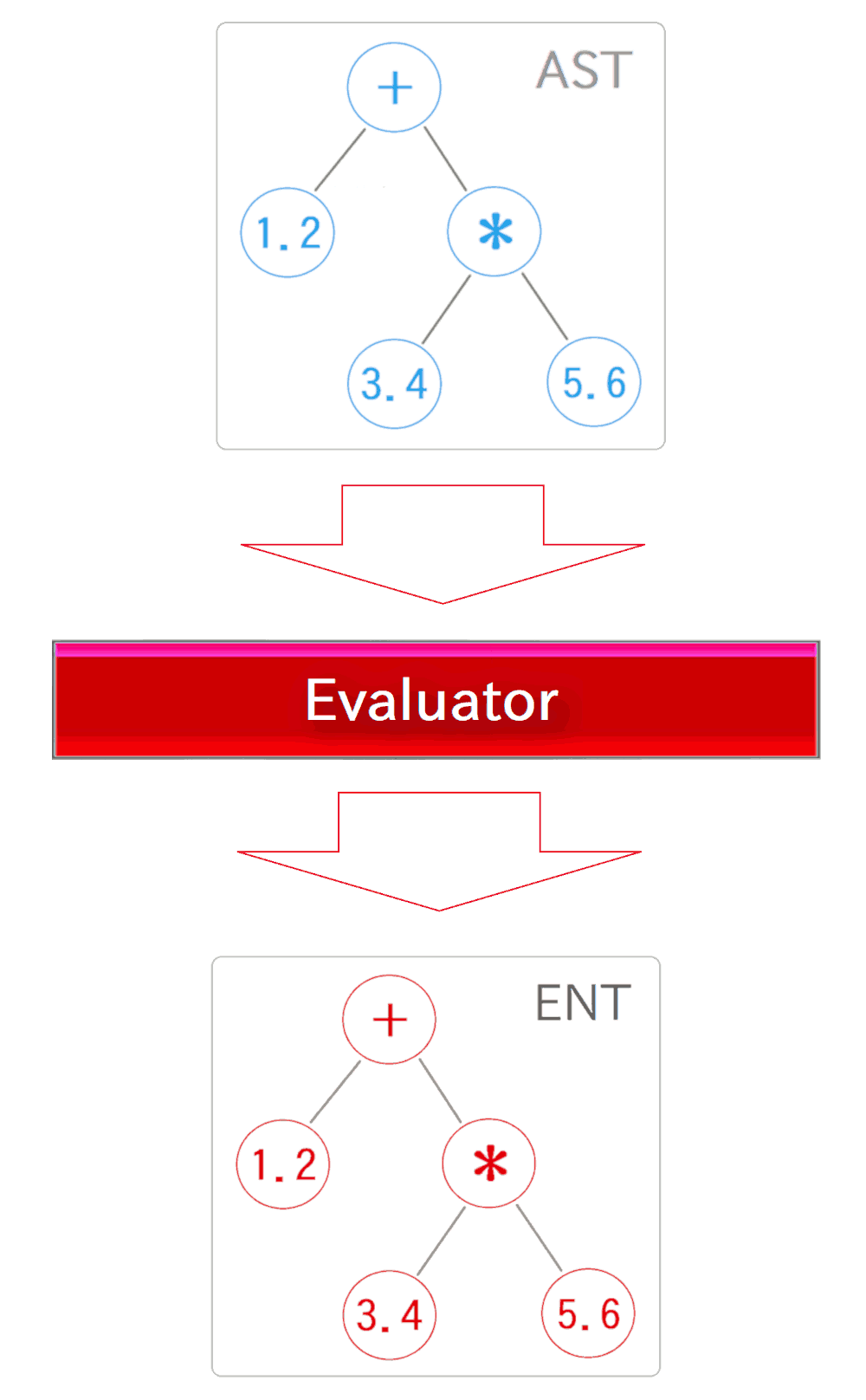
And finally, we get the calculated value of the expression, as the return value of "evaluate" method of the ENT's root node.
For calculating each ENT node's value, it requires a cost to refer so-called "vtable", but it is lighter compared with "switch" statement having many "case"s. So the Evaluator can calculates the value faster than a naive implementation of tree walker.
Here you may have question that:
The process to construct a ENT should contain many branch instructions, to create each instance of EvaluatorNode's subclass suitable for the type of each AstNode. In addition, creating many node instances requires memory allocations many time. Isn't it heavy compared with a simple tree walker?
The above counterargument is correct. The method we explained in this section can "calculate" the value faster, but process to "construct" a ENT is relatively heavy, so it totally gives no advantage compared with a simple tree walker, when you calculate the expression only once.
However, when you calculate the same expression repeatedly, it gives the great advantage, as we explain in the next section.
Now we have explained almost all of the whole structure of Exevalator. In the remained part of this article, we will do some supplementary explanations.
The first topic is: behaviour when the same expression is inputted repeatedly. For example, when you want to draw a curve of (x, f(x)) where f(x) is inputted by the user, it is necessary to calculate f(x) repeatedly, by changing x little by little. For another example, when you want to convert all elements of an array by the same expression, which is inputted by user, it is necessary to process the conversion expression repeatedly for all elements in the array. So, it is not rare situation at all.
For the same expression, at each stage we explained in this article, you get completely same results: same tokens, the same AST, and the same ENT.
Hence, Exevalator internally caches the ENT instance of last evaluated expression, and reuse it when the same expression is inputted. By this caching, Exevalator can skip all heavy processes: lexical analysis, parsing, and construction of ENT. So it works over 100 times faster than "uncached" behaviour.
Here you may have a question that:
When we call "evaluate" method of the completely same ENT ('s node) instance, doesn't it return the same value?
The answer is no. See the next section.
Next topic is: how the exevalator calculates an expression, in which variables are used.
In the ENT, an instance of VariableEvaluatorNode class is used for a node of variable. This node instance is storing the address, not value, of the variable. The address is gotten by referencing the variable table when the Evaluator constructs the ENT.
When "evaluate" method of VariableEvaluatorNode instance is called, it access to the memory (= double-type array) and read the value dynamically, and returns it.
Hence, the return value(s) of the same VariableEvaluatorNode instance varies when the value in the memory is modified. So there is no problem to reuse the same EST instance. It always returns the value calculating by using current values of variables.
How about function calls? It is similar to accesses to variables, but little different.
On Exevalator, a function is implemented as an object of a class implementing Exevalator.FunctionInterface. The developer of the app using Exevalator implement it, and register its instance to Exevalator.
The registered function object is stored in the function table, and referred when the Evaluator constructs the ENT, to be stored into an instance of FunctionEvaluatorNode class.
The FunctionEvaluatorNode is a node for calling a function. When its "evaluate" method is called, it calls "invoke" method of the internally stored function object, with passing values of child nodes as arguments. The "invoke" method is declared in FunctionInterface, and the app developer implement the process of the function in it. The return value of the "invoke" method will be returned as the value of FunctionEvaluatorNode instance.
As the above, Exevalator calls a registered function internally.
The order of topics may reverted from as they should are.
The last topic is (though we had already explained almost all of it): How variables and functions are registered to Exevalator.
Exevalator class has a double-type array field, as the memory for storing values of variables. In addition, Exevalator also has a HashMap-type field for mapping each variable name to each variable address, where the address means that the array index at which the value of the variable is stored.
An app developer can declare a new variable by calling "declareVariable(String name)" method of Exevalator. Then, Exevalator finds an unused address, and register pair of the address and the name to the variable table. It will be refered when a ENT is constructed, as we already explained.
When the app developer modify the value of the variable by calling "writeVariable(String name, double value)" method, Exevalator get the address (= array index) of the variable by referencing the variable table, and updates the value of the element in the "memory" array.
For functions, Exevalator also has a HashMap-type field for mapping each function name to each function object. When the app developer register a function by calling "connectFunction(String name, FunctionInterface functionObject)", Exevalator registeres the pair of the name and the function object to the function table. It will be refered when a ENT is constructed, as we explained in the previous section.
---
In this article, we explained the internal architecture of Exevalator. When there is additional information about Exevalator, we will report it in this "RINEARN News" category.